哈希

两数之和

题目

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

分析

已知目标和一个数，我们只需要记录这个数另一个互补的数是否也在，所以要检验是否存在的最好方法就是利用之前已经访问过的数，其已经被存入哈希表。

O(n)，T(n)

class Solution {
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer, Integer> map = new HashMap<>();
        int[] ans = new int[2];
        for (int i = 0; i< nums.length;i++) {
            int tmp = target - nums[i];
            if (map.containsKey(tmp)) {
                ans[0] = i;
                ans[1] = map.get(tmp);
                break;
            }
            map.put(nums[i], i);
        }
        return ans;
    }
}

字母异位词分组

题目

****

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]

输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

分析

只是位置发生改变，但是字母的组成不会改变，只需要分析各类字母的数量。

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String, List<String>> map = new HashMap<>();
        for (int i = 0; i < strs.length; i++) {
            int[] count = new int[26];
            char[] str = strs[i].toCharArray();
            for (Character c : str) {
                int index = c - 'a';
                count[index]++;
            }
            StringBuilder sb = new StringBuilder();
            for (int j = 0; j < count.length; j++) {
                if (count[j] != 0) {
                    sb.append((char) 'a' + j); // 特征字母
                    sb.append(count[j]); // 特征次数
                }
            }
            String s = sb.toString();

            List<String> list = map.getOrDefault(s, new ArrayList<String>());
            list.add(strs[i]);
            map.put(s, list);

        }
        return new ArrayList<List<String>>(map.values());
    }
}

最长连续序列

题目

````__

输入：nums = [100,4,200,1,3,2]

输出：4

解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

分析

class Solution {
    /**
     * 我们要以n的复杂度解决，只能遍历几次数组，那么就需要利用之前的信息。
     * 如果当前的数字的邻域刚好有之前出现过的数字，
     * 则以当前数字所在序列就是这个+1
     * @param nums
     * @return
     */
    public int longestConsecutive(int[] nums) {
        int ans = 0;
        Set<Integer> set = new HashSet<>();
        for (Integer integer : nums) {
            set.add(integer);
        }
        for (Integer i : set) {
            if(!set.contains(i-1)){
                // 从最底层开始，序列中间的数不会被重复计算
                int len = 1;
                int _i = i;
                while (set.contains(_i+1)) {
                    len++;
                    _i++;
                }
                ans = Math.max(ans, len);
            }
        }
        return ans;
    }
}

双指针

移动零

题目

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。请注意 ，必须在不复制数组的情况下原地对数组进行操作。

输入: nums = [0,1,0,3,12]

输出: [1,3,12,0,0]

分析

如果有这样一串数

10034050

左指针指向已处理的尾部，右指针指向待处理的头部。我们可以将左右内部视为一个全为“0”的区间（虽然实际不是）

如果右非零，说明可以填充过去。然后"移动"这个0序列区间。

否则扩大右侧0区间。最后移动到末尾时，从左侧开始全部重新填一般0

O(n）

class Solution {
    public void moveZeroes(int[] nums) {
        int left = 0, right = 0;
        for (int i = 0; i < nums.length; i++) {
            if(nums[i]!=0){
                continue;
            }
            left = i;
            right = i+1;
            break;
        }
        while (right<nums.length) {
            if(nums[right]!=0){
                nums[left++] = nums[right++];
                continue;
            }
            right++;
        }
        while (left<nums.length) {
            nums[left++]=0;
        }
    }
}

盛最多水的容器

题目

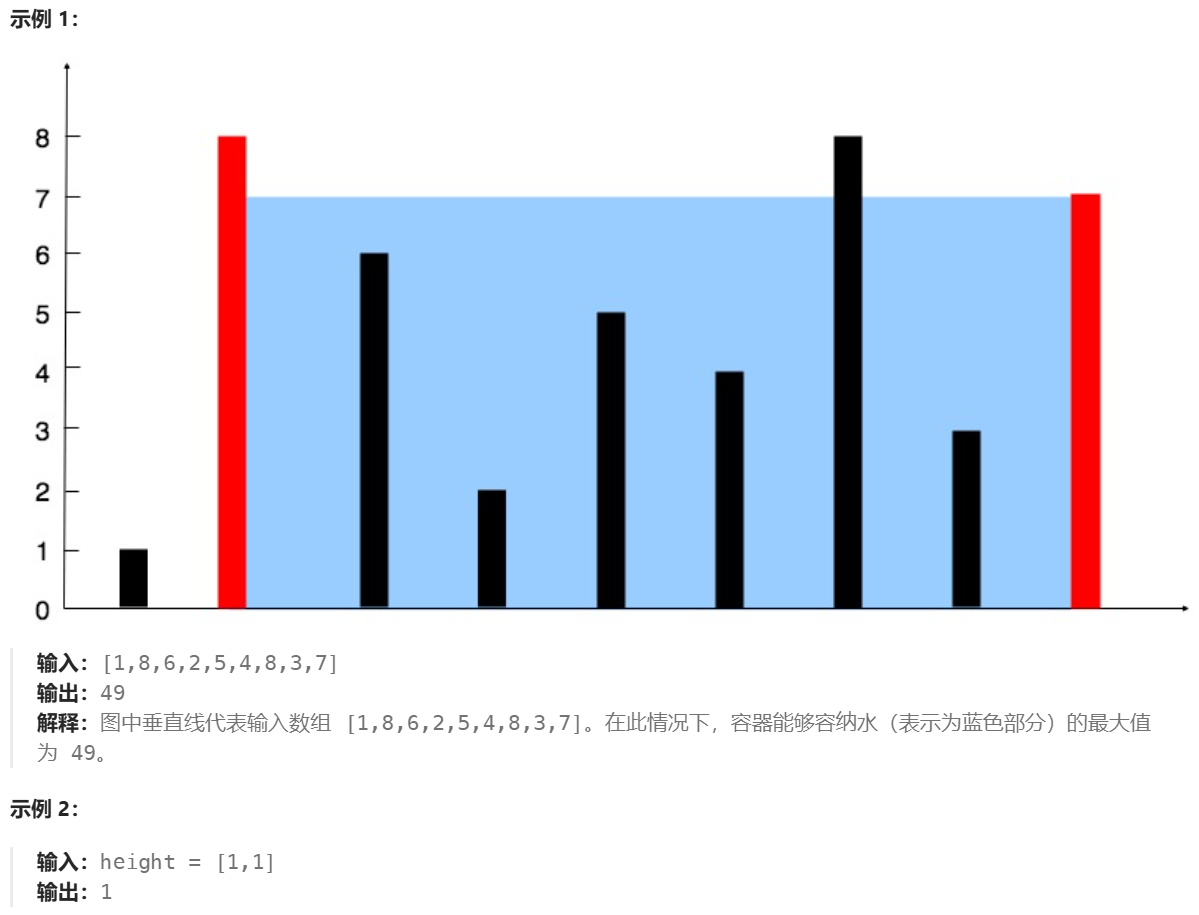
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

分析

为什么双指针的做法是正确的？

双指针代表了什么？

双指针代表的是 可以作为容器边界的所有位置的范围。在一开始，双指针指向数组的左右边界，表示 数组中所有的位置都可以作为容器的边界，因为我们还没有进行过任何尝试。在这之后，我们每次将 对应的数字较小的那个指针 往 另一个指针 的方向移动一个位置，就表示我们认为 这个指针不可能再作为容器的边界了。

由于指针向内部移动，水的宽度一定在减少，水的高度取决于最低的高度，所以要增加高度，必要条件是丢弃当前最低的高度，否则一定是往减少的方向发展的。

另一个方面来说，我们的问题由这些高度的集合组成，当丢弃掉一个高度后，说明我们已经比较过了这个集合的最大取值，并且这个集合不会再参与后续问题。

class Solution {
    public int maxArea(int[] height) {
        int left = 0, right = height.length-1;
        int ans = 0;
        while (left<right) {
            ans = Math.max(ans,  Math.min(height[left],height[right])*(right-left));

            if(height[left]<height[right]){
                left++;
            }else{
                right--;
            }
        }
        return ans;
    }
}

三数之和

题目

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

输入：nums = [-1,0,1,2,-1,-4]

输出：[[-1,-1,2],[-1,0,1]]

解释：

nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。

nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。

nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。

不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。

注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]

输出：[]

解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]

输出：[[0,0,0]]

解释：唯一可能的三元组和为 0 。

分析

可以看作第一层循环选择两数之和的一个target，第二层循环就是找两数之和，不过要避免重复解，以及两个重复数可以被达成目标的情况。这里是哈希的做法。双指针还没学会。。。

以下代码的实际运行效率还是差了点，但是能过，复杂度也算O(n^2)。

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();
        Set<Integer> used_k = new HashSet<>();
        Arrays.sort(nums);
        for(int k = 0;k<nums.length-2;k++){
            if(used_k.contains(nums[k])){ // 若存在重复，则提前出现的数应该包含后出现的重复数的解集
                continue;
            }
            used_k.add(nums[k]);
            int target = -nums[k];
            Set<Integer> map = new HashSet<>();
            Set<Integer> used = new HashSet<>();
            for(Integer i=k+1;i<nums.length;i++){
                if(used.contains(nums[i])){
                    continue;
                }
                int t = target - nums[i];
                if(map.contains(t)){
                    List<Integer> _ans = new ArrayList<>();
                    _ans.add(nums[k]);
                    _ans.add(nums[i]);
                    _ans.add(t);
                    used.add(nums[i]);
                    used.add(t);
                    ans.add(_ans);
                }
                map.add(nums[i]);
            }
        }
        return ans;
    }
}

单调栈

接雨水

题目

分析

双向单调栈，感觉有水的想象力就很明显了

class Solution {
    private int[] height;

    public int trap(int[] height) {
        if (height.length < 3) {
            return 0;
        }
        this.height = height;
        List<Integer> left = new ArrayList<>();
        List<Integer> right = new ArrayList<>();
        {
            int left_height = 0;
            for (int i = 0; i < height.length; i++) {
                if (left_height > height[i]) {
                    continue;
                }
                left.add(i);
                left_height = height[i];
            }
        }
        {
            int right_height = 0;
            int left_max = left.getLast();
            for (int i = height.length - 1; i >= left_max; i--) {
                if (right_height > height[i]) {
                    continue;
                }
                right.add(i);
                right_height = height[i];
            }
        }
        int ans = 0;
        if (left.size() > 1) {
            int _h = left.getFirst();
            for (int i = 1; i < left.size(); i++) {
                ans += this.getSize(_h, left.get(i));
                _h = left.get(i);
            }
        }
        if (right.size() > 1) {
            int _h = right.getFirst();
            for (int i = 1; i < right.size(); i++) {
                ans += this.getSize(right.get(i), _h);
                _h = right.get(i);
            }
        }
        return ans;
    }

    private int getSize(int l, int r) {
        if (l >= r - 1) {
            return 0;
        }
        int h = Math.min(this.height[l], this.height[r]);
        int res = 0;
        for (int i = l + 1; i < r; i++) {
            res += h - this.height[i];
        }
        return res;
    }
}

矩阵

矩阵置零

题目

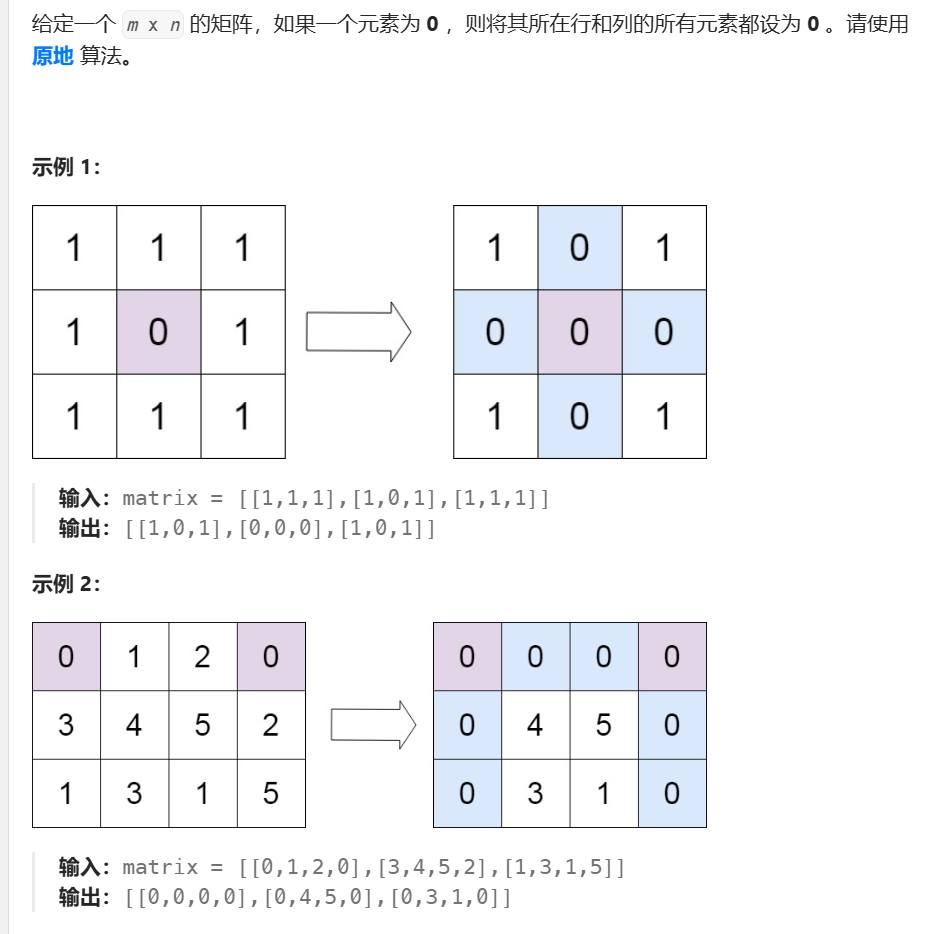
解答

稍微注意一下，如果记录0的点位后，逐个清除，复杂度是O(mn+k(m+n)）,所以需要合并置零，以达到O(mn)

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        Set<Integer> row = new HashSet<>();
        Set<Integer> col = new HashSet<>();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == 0) {
                    row.add(i);
                    col.add(j);
                }
            }
        }
        for (Integer i : row) {
            for (int j = 0; j < n; j++) {
                matrix[i][j] = 0;
            }
        }
        for(int i =0;i<m;i++){
            for(Integer j: col){
                matrix[i][j]=0;
            }
        }
    }
}

螺旋矩阵

题目

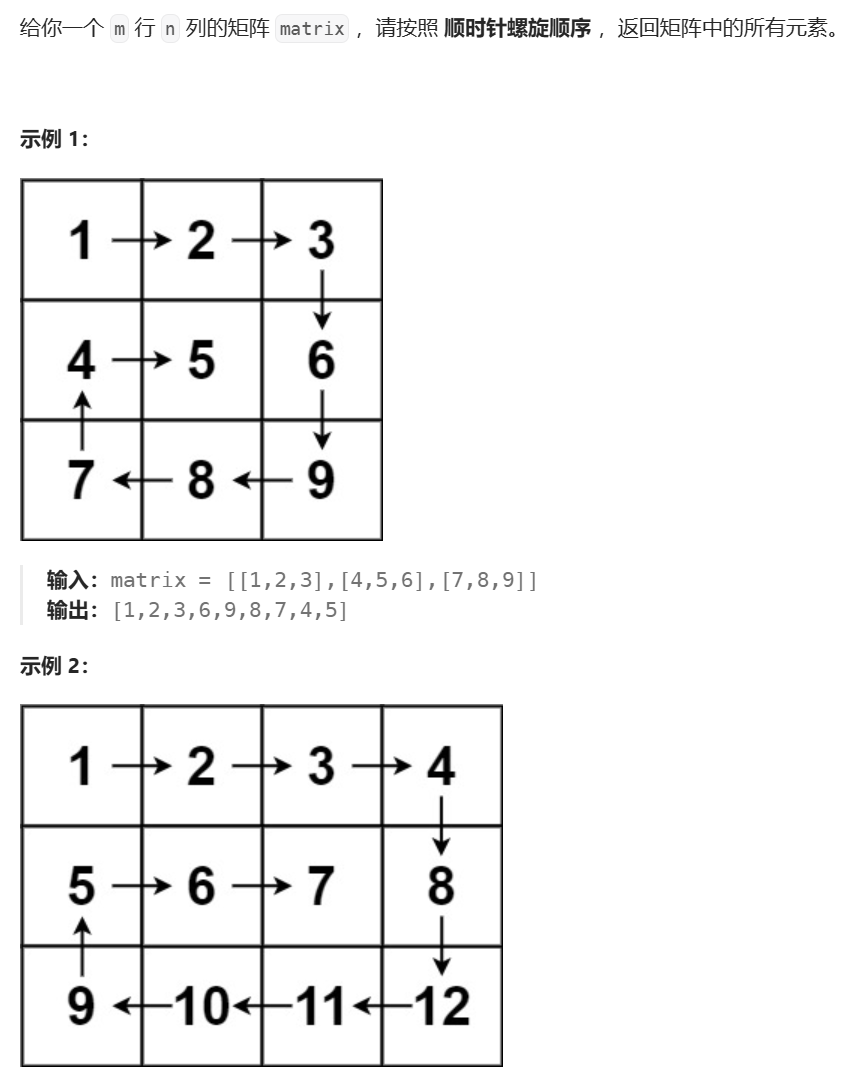
分析

常规的模拟，就不要想着写什么优雅的代码了，直接全部面向过程。

class Solution {
    private int[] dir = new int[] { 0, 1 };
    int max_row, max_col;

    public List<Integer> spiralOrder(int[][] matrix) {
        this.max_row = matrix.length;
        this.max_col = matrix[0].length;
        List<Integer> ans = new ArrayList<>();
        int max_count = matrix.length * matrix[0].length;
        int i = 0, j = -1;
        while (this.max_row!=0&&this.max_col!=0) {
            int row_d = this.dir[0], col_d = this.dir[1], l=0;
            if(col_d!=0){
                while (l++<this.max_col) {
                    j+=col_d;
                    ans.add(matrix[i][j]);
                }
            }else{
                while (l++<this.max_row) {
                    i+=row_d;
                    ans.add(matrix[i][j]);
                }
            }
            turn();
        }
        return ans;
    }

    private void turn() {
        int row_d = this.dir[0], col_d = this.dir[1];
        if (row_d == 0 && col_d == 1) {
            this.dir[0] = 1;
            this.dir[1] = 0;
            this.max_row--;
        } else if (row_d == 1 && col_d == 0) {
            this.dir[0] = 0;
            this.dir[1] = -1;
            this.max_col--;
        } else if (row_d == 0 && col_d == -1) {
            this.dir[0] = -1;
            this.dir[1] = 0;
            this.max_row--;
        } else {
            this.dir[0] = 0;
            this.dir[1] = 1;
            this.max_col--;
        }
    }
}

旋转图像

题目

____``[****](https://baike.baidu.com/item/%E5%8E%9F%E5%9C%B0%E7%AE%97%E6%B3%95)********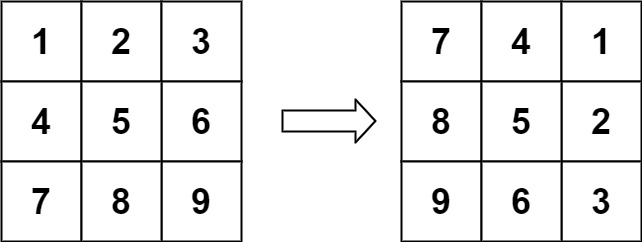

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]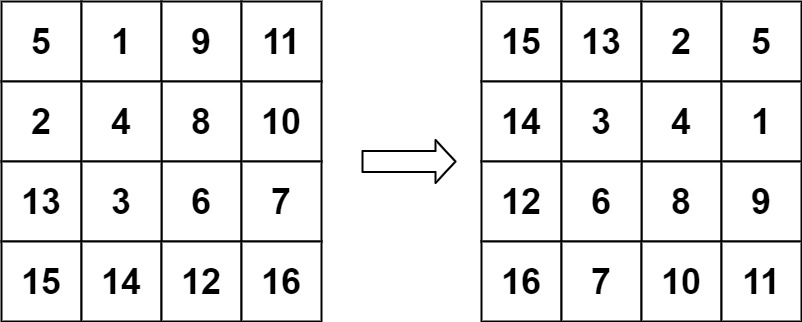

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

• <font style="color:rgba(38, 38, 38, 0.75);background-color:rgb(240, 240, 240);">n == matrix.length == matrix[i].length</font>
• <font style="color:rgba(38, 38, 38, 0.75);background-color:rgb(240, 240, 240);">1 <= n <= 20</font>
• <font style="color:rgba(38, 38, 38, 0.75);background-color:rgb(240, 240, 240);">-1000 <= matrix[i][j] <= 1000</font>

解答

模拟，特性是4点旋转矩阵

class Solution {
    public void rotate(int[][] matrix) {
        /**
         * 起点为k=0,1,2...(k,k),k<=n>>1;
         * 当n=4,l=n-1=3,(0,1)(1,3)(3,2)(2,0)
         * 4点旋转，设(i,j)(j,l-i)(l-i,l-j)(l-j,i)
         * 外层控制点范围[k,k+l)
         */
        int N = matrix.length;
        int max_k = N >> 1;
        int l = N -1;
        for (int k = 0; k < max_k; k++) {
            int n = N - 2 * k;
            int len = n - 1;
            for (int i = k, j = k; j < k + len; j++) {
                int a1 = matrix[i][j], a2 = matrix[j][l - i], a3 = matrix[l - i][l - j], a4 = matrix[l - j][i];
                matrix[i][j] = a4;
                matrix[j][l - i] = a1;
                matrix[l - i][l - j] = a2;
                matrix[l - j][i] = a3;
            }
        }
    }
}

搜索二维矩阵 II

解答

二分

很自然的想到二分，不过注意是区间特性，只能在行内查找

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        /**
         * 每一行就是一段可能重复或不重复的递增区间段，先二分确定行，如果存在行，再二分查找行内
         */
        int m = matrix.length, n = matrix[0].length;
        for (int i = 0; i < m && matrix[i][0] <= target; i++) {
            int left = 0, right = n;
            while (left < right) {
                int mid = (left + right) >> 1;
                if (matrix[i][mid] == target) {
                    return true;
                }
                if (matrix[i][mid] > target) {
                    right = mid;
                } else {
                    left = mid+1;
                }
            }
        }
        return false;
    }
}

Z字形

从左下角开始，如果大就++col,如果小就--y，没出界前找到了就返回true

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] == target) {
                return true;
            }
            if (matrix[x][y] > target) {
                --y;
            } else {
                ++x;
            }
        }
        return false;
    }
}

二分

搜索插入位置

模板题，懒得说。

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0, right = nums.length;
        while (left<right) {
            int mid = (left+right)>>1;
            if(nums[mid]==target){
                return mid;
            }else if(nums[mid]>target){
                right=mid;
            }else{
                left=mid+1;
            }
        }
        // 数组的边界
        if(left>=nums.length){
            return nums.length;
        }
        if(nums[left]>target){
            return left;
        }
        return left+1;
    }
}

搜索二维矩阵

模板题，懒得说

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int left = 0, right = m;
        while (left < right) {
            int mid = (left + right) >> 1;
            // System.out.printf(" mid = %d\n", mid);
            if (matrix[mid][0] <= target && target <= matrix[mid][n - 1]) {
                /** 在行内 */
                int _left = 0, _right = n;
                while (_left < _right) {
                    int _mid = (_left + _right) >> 1;
                    // System.out.printf("_mid = %d\n",_mid);
                    if (matrix[mid][_mid] == target)
                        return true;
                    else if (matrix[mid][_mid] > target) {
                        _right = _mid;
                    } else {
                        _left = _mid + 1;
                    }
                }
                break;
            } else if (matrix[mid][0] > target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return false;
    }
}

在排序数组中查找元素的第一个和最后一个位置

两次模板找边界，边界容易出错。

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int left = 0,right = nums.length;
        while (left<right) {
            int mid= (left+right)>>1;
            if(nums[mid]>=target){
                right = mid;
            }
            else{
                left=mid+1;
            }
        }
        int start = left;
        if(start>=nums.length||nums[start]!=target){
            return new int[]{-1,-1};
        }
        left = 0;
        right = nums.length;
        while (left<right) {
            int mid= (left+right)>>1;
            if(nums[mid]>target){
                right = mid;
            }
            else{
                left=mid+1;
            }
        }
        int end = left;
        if(nums.length==end||nums[end]!=target)
            end--;
        return new int[]{start,end};
    }
}

搜索旋转排序数组

``****``````****``****``````****````````````

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0

输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3

输出：-1

这个先要确定边界k的位置，否则没法将其视为有序数组。

INFO

这里的确定边界和下一题的解题方法是一样的，可以先看看下一题。

然后由于需要logN，不能去复制数组，则只有通过一点数学手段找到数字了

class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length-1;
        while (left<right) {
            int mid = (left+right)>>1;
            if(nums[mid]<=nums[right]){
                right = mid;
            }else{
                left = mid + 1;
            }
        }
        int l = nums.length, bias = left;
        left = 0; right = nums.length-1;
        while (left<right) {
            int mid = (left+right)>>1;
            int _m = (mid+bias)%l;
            if(nums[_m]>=target){
                right = mid;
            }else{
                left = mid+1;
            }
        }
        if(nums[(left+bias)%l]==target){
            return (left+bias)%l;
        }
        return -1;
    }
}

寻找旋转排序数组中的最小值

``````****``

• ````
• ````

``****``****``****``

class Solution {
    public int findMin(int[] nums) {
        int left = 0, right = nums.length - 1;
        while (left < right) {
            int mid = (left + right) >> 1;
            if (nums[mid] <= nums[right]) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return nums[left];
    }
}

滑动窗口

无重复字符的最长子串

class Solution {
    public int lengthOfLongestSubstring(String s) {
        char[] str = s.toCharArray();
        int l = s.length();
        if(l<2){
            return l;
        }
        Map<Character, Integer> set = new HashMap<>();
        int left = 0, right = 0;
        int max_l = 1;
        set.put(str[0],0);
        for(int i=1;i<l;i++){
            if(set.containsKey(str[i])){
                // 如果包含重复字符，就要收缩到重复字符的右边
                int j = left;
                left = set.get(str[i]) + 1;
                while (j<left) {
                    set.remove(str[j++]);
                }
                right = i;
                set.put(str[i], i);
                
            }else{
                // 正常情况扩展右边，并比较最大值
                right++;
                max_l = Math.max(max_l, right-left+1);
                set.put(str[i],i);
            }
        }
        return max_l;
    }
}

找到字符串中所有字母异位词

class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        // 初始化
        int[] count = new int[26];
        int l = s.length();
        char[] str = s.toCharArray();
        char[] _p = p.toCharArray();
        int p_l  = p.length();
        List<Integer> ans = new ArrayList<>();
        int[] p_count = new int[26];
        if(l<p_l){
            return ans;
        }
        for (int i = 0; i < p_l; i++) {
            count[str[i]-'a']++;
            p_count[_p[i]-'a']++;
        }
        if(isValid(count, p_count))
            ans.add(0);

        int right = p_l;
        int left = 0;
        // 移动固定窗口，维护窗口信息
        while (right<l) {
            count[str[left]-'a']--;
            left++;
            count[str[right]-'a']++;
            right++;
            if(isValid(count, p_count))
                ans.add(left);
        }
        return ans;
    }
    private boolean isValid(int[] a,int[] b){
        for (int i = 0; i < 26; i++) {
            if(a[i]!=b[i])
                return false;
        }
        return true;
    }
}

栈

最小栈

easy target，常数时间就需要内存来维护信息

class MinStack {
    private List<Integer> stack = new ArrayList<>();
    private List<Integer> minStack = new ArrayList<>();

    public MinStack() {
        
    }
    
    public void push(int val) {
        stack.add(val);
        if(minStack.isEmpty()){
            minStack.add(val);
        }else{
            minStack.add(Math.min(minStack.getLast(), val));
        }
    }
    
    public void pop() {
        stack.removeLast();
        minStack.removeLast();
    }
    
    public int top() {
        return stack.getLast();
    }
    
    public int getMin() {
        return minStack.getLast();
    }
}

字符串解码

遇到[就入栈（递归栈），]就出栈，线性遍历一次就够了。

class Solution {
    int i = 0;
    char[] str;
    public String decodeString(String s) {
        str = s.toCharArray();
        StringBuilder sb = new StringBuilder();
        int l = s.length();
        for(;i<l;i++){
            if(str[i]>='a'&&str[i]<='z'){
                sb.append(str[i]);
            }else if(str[i]>='0'&&str[i]<='9'){
                int num_left = i;
                StringBuilder num = new StringBuilder();
                num.append(str[i]);
                while (str[++i]!='[') {
                    num.append(str[i]);
                }
                Integer ratio = new Integer(num.toString());
                // 现在i指向的是[
                i++;
                String sub_str = decodeString(s);
                // System.out.printf("将要返回%d倍的",ratio);
                // System.out.println(sub_str);
                while (ratio-->0) {
                    sb.append(sub_str);
                }
            }else {
                return sb.toString();
            }
        }
        return sb.toString();
    }
}

每日温度

显然的单调栈。

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int[] ans = new int[temperatures.length];
        int l = temperatures.length;
        List<Integer> stack = new LinkedList<>();
        for (int i = 0; i < l; i++) {
            while (!stack.isEmpty()) {
                int top = stack.getLast();
                if (temperatures[top] < temperatures[i]) {
                    ans[top] = i - top;
                    stack.removeLast();
                }else{
                    break;
                }
            }
            stack.add(i);
        }
        return ans;
    }
}

有效的括号

注意顺序

class Solution {
    public boolean isValid(String s) {
        char[] str = s.toCharArray();
        List<Character> stack = new LinkedList<>();
        for (char ch : str) {
            switch (ch) {
                case '(':
                case '{':
                case '[':
                    stack.add(ch);
                    break;
                case ')':
                    if(!stack.isEmpty()&&stack.getLast()=='('){
                        stack.removeLast();
                    }else{
                        return false;
                    }
                    break;
                case '}':
                    if(!stack.isEmpty()&&stack.getLast()=='{'){
                        stack.removeLast();
                    }else{
                        return false;
                    }
                    break;
                case ']':
                    if(!stack.isEmpty()&&stack.getLast()=='['){
                        stack.removeLast();
                    }else{
                        return false;
                    }
                    break;
                default:
                    break;
            }
        }
        if (stack.isEmpty()) {
            return true;
        }
        return false;
    }
}

链表

相交链表

能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

显然尾部要合并，然后可以算出长度，让两边长度相等后，再逐个找是否相同。

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        int la = getLen(headA);
        int lb = getLen(headB);
        if(la>lb){
            return findCommon(headA, headB, la - lb);
        }
        return findCommon(headB, headA, lb-la);
    }
    private int getLen(ListNode a){
        if(a==null)
            return 0;
        int count = 1;
        while (a.next!=null) {
            a = a.next;
            count++;
        }
        return count;
    }
    private ListNode findCommon(ListNode lon, ListNode shor, int derta){
        while (derta-->0) {
            lon = lon.next;
        }
        while (lon!=shor) {
            lon = lon.next;
            shor = shor.next;
        }
        return lon;
    }
}

反转链表

简单的变量交换。。

class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null)
            return null;
        if(head.next==null)
            return head;
        ListNode pre = null, post;
        while (head!=null) {
            post = head.next;
            head.next = pre;
            pre = head;
            head = post;
        }
        return pre;
    }
}

回文链表

可以将后半段反转过来，再逐个对比看是否相等。

怎么找中间的反转点：快慢指针

class Solution {
    public boolean isPalindrome(ListNode head) {
        if (head.next == null) {
            return true;
        }
        if (head.next.next == null) {
            return head.val == head.next.val;
        }
        return reverseSolution(head);
    }

    private boolean reverseSolution(ListNode head) {
        ListNode fast = head, slow = head;
        // 如果fast变为null，说明长度为偶数
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        ListNode end = reverseList(slow);
        return isSame(head, end);
    }

    private ListNode reverseList(ListNode head) {
        if (head == null)
            return null;
        if (head.next == null)
            return head;
        ListNode pre = null, post;
        while (head != null) {
            post = head.next;
            head.next = pre;
            pre = head;
            head = post;
        }
        return pre;
    }

    private boolean isSame(ListNode a, ListNode b) {
        while (a != null && b != null) {
            if (a.val != b.val)
                return false;
            a = a.next;
            b = b.next;
        }
        return true;
    }
}

环形链表

典。

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head, slow = head;
        int s = 0;
        while (fast!=null && fast.next!=null) {
            fast  = fast.next.next;
            slow = slow.next;
            ++s;
            if(fast == slow){
                fast = head;
                return true;
            }
        }
        return false;
    }
}

环形链表 II

太典了。

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast = head, slow = head;
        int s = 0;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            ++s;
            if (fast == slow) {
                fast = head;
                while (fast!=slow) {
                    fast = fast.next;
                    slow = slow.next;
                }
                return fast;
            }
        }
        return null;
    }
}

合并两个有序链表

”简单题“，但是有点烦人。

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        if (list1 == null && list2 == null)
            return null;
        if (list1 == null)
            return list2;
        if (list2 == null)
            return list1;

        ListNode head, tail, tmp;
        if (list1.val > list2.val) {
            head = list2;
            tmp = list2.next;
            list2.next = null;
            list2 = tmp;
        } else {
            head = list1;
            tmp = list1.next;
            list1.next = null;
            list1 = tmp;
        }
        tail = head;
        while (list1 != null && list2 != null) {
            if (list1.val > list2.val) {
                tmp = list2.next;
                list2.next = null;
                tail.next = list2;
                tail = tail.next;
                list2 = tmp;
            } else {
                tmp = list1.next;
                list1.next = null;
                tail.next = list1;
                tail = tail.next;
                list1 = tmp;
            }
        }
        if (list1 == null && list2 != null)
            tail.next = list2;
        else if (list2 == null && list1 != null)
            tail.next = list1;
        return head;
    }
}

/**
 * @param {ListNode} list1
 * @param {ListNode} list2
 * @return {ListNode}
 */
var mergeTwoLists = function (list1, list2) {
    if (list1 == null)
        return list2;
    if (list2 == null)
        return list1;
    var listhead;
    if (list1.val < list2.val) {
        var tmp = list1.next;
        list1.next = null;
        listhead = list1;
        list1 = tmp;
    } else {
        var tmp = list2.next;
        list2.next = null;
        listhead =list2
        list2 = tmp;
    }
    var listtail = listhead;
    while (list1 != null && list2 != null) {
        if (list1.val < list2.val) {
            var tmp = list1.next;
            list1.next = null;
            listtail.next = list1;
            list1 = tmp;
        } else {
            var tmp = list2.next;
            list2.next = null;
            listtail.next = list2;
            list2 = tmp;
        }
        listtail = listtail.next;
    }
    if(list1!=null){
        listtail.next = list1;
    }
    else{
        listtail.next = list2;
    }
    return listhead;
};

两数相加

，emm，还是有点小烦人的。

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        int add = 0;
        ListNode head, tail, tmp;
        {
            int res = l1.val + l2.val + add;
            l1 = l1.next;
            l2 = l2.next;
            add = res / 10;
            head = new ListNode(res % 10);
            tail = head;
        }

        while (l1 != null && l2 != null) {
            int res = l1.val + l2.val + add;
            l1 = l1.next;
            l2 = l2.next;
            add = res / 10;
            tmp = new ListNode(res % 10);
            tail.next = tmp;
            tail = tmp;
        }
        if (l1 == null) {
            l1 = l2;
        }
        while (add != 0) {
            if (l1 == null) {
                tail.next = new ListNode(add);
                break;
            }
            int res = l1.val + add;
            l1 = l1.next;
            add = res / 10;
            tmp = new ListNode(res % 10);
            tail.next = tmp;
            tail = tmp;
        }
        if (l1 != null) {
            tail.next = l1;
        }
        return head;
    }
}

删除链表的倒数第 N 个结点

实际上不可能操作数更小了，只是确实某种意义上来说是一次遍历。

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode right = head, left, before_left = null;
        while (n-->0) {
            right = right.next;
        }
        left = head;
        while (right!=null) {
            right = right.next;
            before_left = left;
            left = left.next;
        }
        if(before_left==null){
            return left.next;
        }
        before_left.next = left.next;
        return head;
    }
}

两两交换链表中的节点

class Solution {
    public ListNode swapPairs(ListNode head) {
        if (head == null)
            return null;
        if (head.next == null)
            return head;
        ListNode a = head, b = head.next, listHead, listTail;
        a.next = b.next;
        b.next = a;
        listHead = b;
        listTail = a;
        while (listTail.next != null) {
            a = listTail.next;
            if (a.next == null)
                break;
            b = a.next;
            listTail.next = b;
            a.next = b.next;
            b.next = a;
            listTail = a;
        }
        return listHead;
    }
}

随机链表的复制

class Solution {
    public Node copyRandomList(Node head) {
        Map<Node, Node> map = new HashMap<>();
        Node tmp = head, last=null, first=null;
        while (tmp!=null) {
            Node new_node = new Node(tmp.val);
            if(last!=null)
                last.next = new_node;
            else
                first = new_node;
            map.put(tmp, new_node);
            tmp = tmp.next;
            last = new_node;
        }
        tmp = head;
        while (tmp!=null) {
            if(tmp.random!=null){
                map.get(tmp).random = map.get(tmp.random);
            }
            tmp = tmp.next;
        }
        return first;
    }
}

LRU 缓存

O(1)的操作，那只有引入hash表了，但是算法题又不能之间让你用LinkedHashTable，所以要自己构造链表及其节点。

class LRUCache {
    Map<Integer, Node> map = new HashMap<>();
    private final int capcacity;

    private class Node {
        int key;
        int value;
        Node pre;
        Node next;

        public Node(int v, int k) {
            this.value = v;
            this.key = k;
            this.pre = null;
            this.next = null;
        }
    }

    private int size;
    Node head, tail;

    public LRUCache(int capacity) {
        this.capcacity = capacity;
        this.head = null;
        this.tail = null;
    }

    public int get(int key) {
        if (map.containsKey(key)) {
            Node node = map.get(key);
            toFirst(node);
            return node.value;
        }
        return -1;
    }

    public void put(int key, int value) {
        if (map.containsKey(key)) {
            Node node = map.get(key);
            toFirst(node);
            node.value = value;
        } else if (size == 0) {
            Node node = new Node(value, key);
            map.put(key, node);
            head = node;
            tail = node;
            size = 1;
        } else if (size < capcacity) {
            Node node = new Node(value, key);
            map.put(key, node);
            head.pre = node;
            node.next = head;
            head = node;
            size++;
        } else {
            map.remove(tail.key);
            tail = tail.pre;
            Node node = new Node(value, key);
            map.put(key, node);
            if (tail == null) {
                head = node;
                tail = node;
            } else {
                tail.next = null;
                head.pre = node;
                node.next = head;
                head = node;
            }
        }
    }

    private void toFirst(Node node) {
        if (node == head) {
            return;
        }
        Node pre = node.pre;
        Node next = node.next;
        if (pre != null) {
            pre.next = next;
        }
        if (next != null) {
            next.pre = pre;
        } else {
            tail = pre;
        }
        node.pre = null;
        node.next = head;
        head.pre = node;
        head = node;
    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

排序链表

O(n log n) 时间复杂度就想到归并，所以还得先写一个合并有序链表，自顶向下是占用n的空间

常数空间需要自底向上。以下是自底向上的做法。

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var sortList = function (head) {
    var length = 0;
    for (var tmp = head; tmp != null; tmp = tmp.next)length++;
    var dummyRoot = new ListNode(0, head);
    // 子串长度从单个节点开始，这样就可以利用merge进行排序
    for (var l = 1; l < length; l <<= 1) {
        var pre = dummyRoot, sub_h = dummyRoot.next;
        while (sub_h != null) {
            var sub_tail = sub_h;
            // 找到第一个子串尾部
            for (var i = 1; i < l && sub_tail?.next != null; i++, sub_tail = sub_tail.next);
            var sub_h2 = sub_tail.next;
            sub_tail.next = null; // 分割子串之间
            var sub_tail2 = sub_h2;
            // 找到第二个子串尾部
            for (var i = 1; i < l && sub_tail2?.next != null; i++, sub_tail2 = sub_tail2.next);
            // 下一轮开头就是这次子串2尾部的下一个
            var next = null;
            if(sub_tail2!=null){
                next = sub_tail2.next;
                sub_tail2.next = null;
            }
            var mergedList = merge(sub_h, sub_h2);
            pre.next = mergedList;
            while(pre.next!=null) pre = pre.next;
            // 下一轮开头就是这次子串2尾部的下一个
            sub_h = next;
        }
    }
    return dummyRoot.next;
};
/**
 * @param {ListNode} list1
 * @param {ListNode} list2
 */
function merge(list1, list2) {
    if (list1 == null)
        return list2;
    if (list2 == null)
        return list1;
    var listhead;
    if (list1.val < list2.val) {
        var tmp = list1.next;
        list1.next = null;
        listhead = list1;
        list1 = tmp;
    } else {
        var tmp = list2.next;
        list2.next = null;
        listhead = list2
        list2 = tmp;
    }
    var listsub_tail = listhead;
    while (list1 != null && list2 != null) {
        if (list1.val < list2.val) {
            var tmp = list1.next;
            list1.next = null;
            listsub_tail.next = list1;
            list1 = tmp;
        } else {
            var tmp = list2.next;
            list2.next = null;
            listsub_tail.next = list2;
            list2 = tmp;
        }
        listsub_tail = listsub_tail.next;
    }
    if (list1 != null) {
        listsub_tail.next = list1;
    }
    else {
        listsub_tail.next = list2;
    }
    return listhead;
}

技巧

只出现一次的数字

同样的数异或为0

class Solution {
    public int singleNumber(int[] nums) {
        int a = 0, l = nums.length;
        for (int i = 0; i < l; i++) {
            a^=nums[i];
        }
        return a;
    }
}

数组

最大子数组和

分治是很精妙，但是实际用起来的时间消耗比dp大。。。

class Solution {
    public int maxSubArray(int[] nums) {
        return divSolution(nums);
    }

    private int dpSolution(int[] nums) {
        int l = nums.length;
        int[] dp = new int[l + 1];
        int ans = nums[0];
        for (int i=0;i<l;i++) {
            dp[i+1] = Math.max(nums[i], nums[i]+dp[i]);
            ans = Math.max(ans, dp[i+1]);
        }
        return ans;
    }

    class Node {
        int leftMax, rightMax, max, sum;
        Node(int l, int r, int max, int sum){
            this.leftMax = l;
            this.rightMax = r;
            this.max = max;
            this.sum = sum;
        }
        Node(){

        }
    }
    int[] nums;
    private int divSolution(int[] nums){
        this.nums = nums;
        Node node = resolve(0, nums.length-1);
        return node.max;
    }
    private Node resolve(int left, int right){
        if(left==right){
            return new Node(nums[left],nums[left], nums[left], nums[left]);
        }
        int mid = (left+right)>>1;
        Node leftNode = resolve(left, mid);
        Node rightNode = resolve(mid+1, right);
        Node node = new Node();
        node.sum = leftNode.sum +rightNode.sum;
        node.leftMax = Math.max(leftNode.leftMax, rightNode.leftMax+leftNode.sum);
        node.rightMax = Math.max(rightNode.rightMax, leftNode.rightMax+rightNode.sum);
        node.max = Math.max( leftNode.rightMax+rightNode.leftMax,Math.max(leftNode.max, rightNode.max));
        return node;
    }
}

合并区间

典

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, (a, b)->{
            return a[0] - b[0];
        });
        List<int[]> list = new ArrayList<>();
        int start = intervals[0][0];
        int end = intervals[0][1];
        for(int i=1;i<intervals.length;i++){
            int[] item = intervals[i];
            if(item[0]<=end){
                end = Math.max(end, item[1]);
            }else{
                list.add(new int[]{start, end});
                start = item[0];
                end = item[1];
            }
        }
        list.add(new int[]{start, end});
        int[][] ans = new int[list.size()][];
        for (int i=0;i<ans.length;i++) {
            ans[i] = list.get(i);
        }
        return ans;
    }
}

class Solution {
    public void rotate(int[] nums, int k) {
        int l = nums.length;
        int[] tmp = new int[l];
        for (int i = 0; i < tmp.length; i++) {
            tmp[i] = nums[i];
        }
        for (int i = 0; i < tmp.length; i++) {
            int index = (i+k);
            while(index>=l)
                index -=l;
            nums[index] = tmp[i];
        }
    }
}

// 待做

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int l = nums.length;
        int[] right = new int[l];
        right[l-1]=1;
        for (int i = l-2; i>=0; i--) {
            right[i] = right[i+1]*nums[i+1];
        }
        int left = 1;
        for (int i = 0; i < l; i++) {
            int tmp = nums[i];
            nums[i] = left * right[i];
            left*=tmp;
        }
        return nums;
    }
}

class Solution {
    public int firstMissingPositive(int[] nums) {
        int l = nums.length;
        // 找到第一个连续的正数区间末尾,这个区间是[1,N]的子区间
        for (int index = 0; index < l; index++) {
            int i = nums[index];
            if (i > 0) {
                if (i <= l) {
                    if (nums[i - 1] != i) {
                        int tmp = nums[i - 1];
                        nums[i - 1] = i;
                        nums[index] = tmp;
                        index--;
                    }else if(index+1!=i){
                        nums[index]=-1;
                    }
                } else
                    nums[index] = -1;
            }
        }
        for (int i : nums) {
            System.out.println(i);
        }
        int i;
        for (i = 0; i < l; i++) {
            if (nums[i] <= 0)
                return i + 1;
        }
        return i+1;
    }
}

贪心

买卖股票的最佳时机

策略：只能买一次最大的，某日能获得的最大利润就是前几天的最低价格开始。

class Solution {
    public int maxProfit(int[] prices) {
        int  l =prices.length;
        int max = 0, min = prices[0];
        for (int j=1;j<l;j++) {
            int i = prices[j];
            if(i<min){
                min = i;
                continue;
            }
            max = Math.max(max, i-min);
        }
        return max;
    }
}

跳跃游戏

典

策略：尽可能的远，因为你能达到>=终点的地方，说明你可以少跳一点达到终点。

class Solution {
    public boolean canJump(int[] nums) {
        int index = 0, lastIndex = -1;
        int l = nums.length;
        while (index!=lastIndex&&index<l) {
            if(index+1==nums.length)
                return true;
            int i = nums[index];
            int r = 0, r_i = 0;
            for(int j = 1;j<=i&&index+j<l;j++){
                int res =  j+nums[index+j];
                if(res>=r){
                    r_i = j;
                    r = res;
                }
            }
            lastIndex = index;
            index += r_i;
        }
        return false;
    }
}

public class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;
        int rightmost = 0;
        for (int i = 0; i < n; ++i) {
            if (i <= rightmost) {
                rightmost = Math.max(rightmost, i + nums[i]);
                if (rightmost >= n - 1) {
                    return true;
                }
            }
        }
        return false;
    }
}

跳跃游戏 II

DP

爬楼梯

class Solution {
    public int climbStairs(int n) {
        int pre_1 = 0, pre_2 = 1, cur = 0;
        for(int i=0;i<n;i++){
            cur = pre_1+pre_2;
            pre_1 = pre_2;
            pre_2= cur;
        }
        return cur;
    }
}

杨辉三角

class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> list = new ArrayList<>();
        {
            List<Integer> a = new ArrayList<>();
            a.add(1);
            list.add(a);
        }
        for (int i = 2; i <= numRows; i++) {
            List<Integer> row = new ArrayList<>();
            List<Integer> last_row = list.get(i-2);
            row.add(1);
            for (int j = 1; j < i-1 ; j++) {
                row.add(last_row.get(j-1)+last_row.get(j));
            }
            row.add(1);
            list.add(row);
        }
        return list;
    }
}

解法1：dp

/**
 * @param {number[]} nums
 * @return {number}
 */
var jump = function(nums) {
    var count = Array.from({length:nums.length},()=>Infinity);
    count[0]=0;
    for(var i=0;i<nums.length;i++){
        for(var j=1;j<=nums[i];j++){
            if(i+j<nums.length)
            count[i+j]=Math.min(count[i+j], count[i]+1);
        }
    }
    return count[nums.length-1];
};

解法2： 贪心

/**
 * @param {number[]} nums
 * @return {number}
 */
var jump = function (nums) {
    var count =0;
    var rightBound = 0;
    var reachAble = nums[0];
    for(var i=0;i<nums.length-1/* 最后一格必定能到达，所以只需要判断之前的层数 */;i++){
        // 基于上一层的最大范围内，跳数共用
        if(i<=rightBound){
            // 更新最大范围
            if(reachAble<i+nums[i]){
                reachAble = i+nums[i];
            }
            if(i==rightBound){
                // 到达上次最大边界，下一层需要的跳数+1
                rightBound = reachAble;
                count++;
            }
        }
    }
    return count;
};

二叉树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal2(TreeNode root) {
        List<TreeNode> stack = new ArrayList<>();
        List<Integer> list = new ArrayList<>();
        Set<TreeNode> set = new HashSet<>();
        if (root != null) {
            stack.add(root);
        }
        while (stack.size() != 0) {
            TreeNode t = stack.getLast();

            if (t.left != null && !set.contains(t.left)) {
                stack.add(t.left);
                continue;
            }
            if (!set.contains(t)) {
                set.add(t);
                list.add(t.val);
            }

            if (t.right != null && !set.contains(t.right)) {
                stack.add(t.right);
                continue;
            }
            stack.removeLast();
        }
        return list;
    }
    private List<Integer> ans = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        solution(root);
        return ans;
    }
    private void solution(TreeNode t){
        if(t==null)
        return;
        solution(t.left);
        ans.add(t.val);
        solution(t.right);
    }
}

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null)
            return 0;
        return Math.max(maxDepth(root.left), maxDepth(root.right))+1;
    }
}

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root==null)
            return null;
        invertTree(root.left);
        invertTree(root.right);
        TreeNode t = root.right;
        root.right = root.left;
        root.left = t;
        return root;
    }
}

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null)
            return null;
        invertTree(root.left);
        invertTree(root.right);
        TreeNode t = root.right;
        root.right = root.left;
        root.left = t;
        return root;
    }

    public boolean isSymmetric(TreeNode root) {
        if (root.left==null&&root.right!=null||root.left!=null&&root.right==null) {
            return false;
        }
        invertTree(root.left);
        return compare(root.left, root.right);
    }
    private boolean compare(TreeNode l, TreeNode r){
        if(l==null&&r!=null||l!=null&&r==null)
            return false;
        return l==null&&r==null||compare(l.left, r.left) && compare(l.right, r.right) && l.val == r.val;
    }
}

直径路径必然经过一种根节点，所以遍历时用每个经过子树节点的长度来更新，并返回最大深度给上层用于更新。

class Solution {
    int D = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        getMax(root);
        return D;
    }
    private int getMax(TreeNode r){
        if(r==null)
            return 0;
        int l1 = getMax(r.left);
        int l2 = getMax(r.right);
        D = Math.max(D, l1+l2);
        return Math.max(l1, l2)+1;
    }
}

二叉树的层序遍历

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> lists = new ArrayList<>();

        List<Pair<TreeNode, Integer>> stack = new LinkedList<>();
        if (root == null)
            return lists;
        stack.add(new Pair<TreeNode, Integer>(root, 0));
        List<Integer> tmp = new ArrayList<>();
        int last_level = 0;
        while (stack.size() != 0) {
            Pair<TreeNode, Integer> p = stack.removeFirst();
            TreeNode t = p.getKey();
            Integer t_l = p.getValue();
            if (t_l != last_level) {
                last_level = t_l;
                lists.add(tmp);
                tmp = new ArrayList<>();
            }
            tmp.add(t.val);
            if (t.left != null)
                stack.add(new Pair(t.left, t_l + 1));
            if (t.right != null)
                stack.add(new Pair(t.right, t_l + 1));
        }
        lists.add(tmp);
        return lists;
    }
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function(root) {
    var valid = (root, left, right) => {
        if(root==null)
            return true;
        if(root.val <= left || root.val >= right)
            return false;
        return valid(root.left, left, root.val) && valid(root.right, root.val, right);
    }
    return valid(root, -Infinity, Infinity);
};

中序遍历

var kthSmallest = function(root, k) {
  var stack = [root];
  var count = 0;
  while(stack.length>0){
    var node = stack[stack.length-1];
    if(node.left!=null){
        stack.push(node.left)
        node.left = null;
        continue;
    }
    count++;
    if(count==k){
        return node.val;
    }
    stack.pop();
    if(node.right!=null){
        stack.push(node.right);
    }
  }  
};

二叉树的右视图

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var rightSideView = function (root) {
    if(root==null){
        return [];
    }
    var queue = [{
        node: root,
        level: 0
    }];
    var ans = []
    while (queue.length > 0) {
        var item = queue.shift();
        if (ans.length == item.level) {
            ans.push(item.node.val);
        } else {
            ans[item.level] = item.node.val;
        }
        if (item.node.left != null) {
            queue.push({
                node: item.node.left,
                level: item.level + 1
            });
        }
        if (item.node.right != null) {
            queue.push({
                node: item.node.right,
                level: item.level + 1
            });
        }
    }
    return ans;
};

/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function(root) {
  if(root==null){
    return null;
  }
  myflat(root);
};
/**
 * @param {TreeNode} root
 * @param {TreeNode} insertion
 * @return {TreeNode} tail
 */
function myflat(root){
  if(root.left==null&&root.right==null){
    return root;
  }
  if(root.left==null&&root.right!=null){
    return myflat(root.right);
  }
  if(root.left!=null&&root.right==null){
    root.right = root.left;
    root.left= null;
    return myflat(root.right);
  }
  var right_tail = myflat(root.right);
  myflat(root.left).right = root.right;
  root.right = root.left;
  root.left = null;
  return right_tail;
}

/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
  var root = new TreeNode(preorder[0], null, null);
  var index = inorder.findIndex(i=>i==root.val);
  if(index>0)
    root.left = buildTree(preorder.slice(1, index+1), inorder.slice(0, index));
  if(index+1<preorder.length)
    root.right = buildTree(preorder.slice(index+1), inorder.slice(index+1));
  return root;
};

var sum;
var target;
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function(root, targetSum) {
    sum = 0;
    target = targetSum;
    search(root);
    return sum;
};
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
function search(root){
    if(root==null){
        return [];
    }
    var arr_l = search(root.left);
    var arr_r = search(root.right);
    var arr = arr_l.concat(arr_r);
    for(let i = 0;i<arr.length;){
        arr[i]+=root.val;
        if(arr[i]==target){
            sum++;
        }
        i++;
    }
    if(root.val==target){
        sum++;
    }
    arr.push(root.val);
    return arr;
}

/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function(root, p, q) {
    var a1 = find(root,p);
    var a2 = find(root, q);
    if(a1.length>a2.length)
     {
        tmp = a2;
        a2 = a1;
        a1 = tmp;
     }
     var i = 0, j = a2.length - a1.length;
     while(i<a1.length){
        if(a1[i]==a2[i+j]){
            return a1[i];
        }
        i++;
     }
    
};
/**
 * @param {TreeNode} root
 * @param {TreeNode} target
 * @return {number[]}
 */
function find(root, target){
    if(root==null)
        return [];
    if(root==target)
        return [target];
    var left = find(root.left,target);
    if(left.length>0){
        left.push(root)
        return left;
    }
    var right = find(root.right,target);
    if(right.length>0){
        right.push(root);
        return right;
    }
    return [];
}

var maxPath;
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxPathSum = function (root) {
    maxPath = -Infinity;
    custom(root);
    return maxPath;
};
/**
 * @param{TreeNode} root
 * @return {number}
 */
function custom(root) {
    var left = -Infinity;
    if (root.left != null)
        left = custom(root.left)
    var right = -Infinity;
    if (root.right != null)
        right = custom(root.right);
    var max_son = Math.max(left, right);
    var tmp = root.val;
    tmp = Math.max(root.val, max_son + root.val);
    maxPath = Math.max(maxPath, tmp, left + right + root.val);
    return tmp;
}

回溯

var ans;
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function(nums) {
    ans = [];
    custom(nums, []);
    return ans;
};
/**
 * @param {number[]} list
 * @param {number[]} tmp
 */
function custom (list, tmp){
    if(list.length==1){
        ans.push(tmp.concat(list));
        return;
    }
    var l = list.length;
    for(var i =0;i<l;i++){
        custom(list.filter(it=>it!=list[i]), tmp.concat([list[i]]));
    }
}

var ans;
var g_nums;
var l;
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsets = function(nums) {
    ans = [];
    g_nums = nums;
    l = g_nums.length;
    for(var i = 0;i<=l;i++){
        custom(0,[],i);
    }
    return ans;
};
/**
 * @param {number} start
 * @param {number[]} tmp
 * @param {number} remain
 */
function custom(start, tmp, remain){
    if(remain==0){
        ans.push(tmp);
        return;
    }
    if(remain<0){
        return;
    }
    for(var i = start;i<l;i++){
        custom(i+1, tmp.concat([g_nums[i]]), remain-1);
    }

}

var ans;
var map = [,,"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"];
/**
 * @param {string} digits
 * @return {string[]}
 */
var letterCombinations = function(digits) {
    ans =[];
    if(digits.length)
    custom(digits, "");
    return ans;
};
/**
 * @param {string} list
 * @param {string} tmp
 */
function custom(list,tmp){
    if(list.length==0){
        ans.push(tmp);
        return;
    }
    var li = map[Number(list.charAt(0))];
    for(var i=0;i<li.length;i++){
        custom(list.slice(1),tmp+li.charAt(i));
    }
}

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function(candidates, target) {
    if(candidates.length==0){
        return [];
    }
    if(target)
    var ans = [];
    for(var i = 0; i<candidates.length;i++){
        var el = candidates[i];
        if(el>target)
            continue;
        if(el==target){
            ans.push([target]);
            continue;
        }
        var sub = combinationSum(candidates.slice(i), target-el);
        if(sub.length!=0){
            sub.forEach(i=>{
                ans.push([el,...i])
            })
        }
    }
    return ans;
};

var map;
var target;
var tag;
var diri = [-1,0,1,0], dirj=[0,1,0,-1];
var w,h;
/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function(board, word) {
    tag = board.map(i=>i.map(i=>1));
    map = board;
    target = word;
    h = board.length;
    w = board[0].length;
    for(var i = 0;i<h;i++){
        for(var j=0;j<w;j++){
            if(tag[i][j]&&board[i][j]==word[0]){
                if(custom(i,j,0)){
                    return true;
                }
            }
        }
    }
    return false;
};
function custom (i,j,index){
    if((i<0||i>=h||j<0||j>=w)){
        return false;
    }
    if(map[i][j]!=target[index]||tag[i][j]==0){
        return false;
    }
    if(index==target.length-1){
        return true;
    }
    tag[i][j]=0;
    for(var k = 0;k<4;k++){
        if(custom(i+diri[k],j+dirj[k],index+1)){
            return true;
        }
    }
    tag[i][j]=1;
    return false;
}

/**
 * @param {string} s
 * @return {string[][]}
 */
var partition = function(s) {
    var l = s.length;
    if(l==1){
        return [[s]];
    }
    var ans = test(s)?[[s]]:[];
    for(var i =1;i<l;i++){
        var sub = s.slice(0,i);
        if(!test(sub)){
            continue;
        }
        var sol = partition(s.slice(i,l));
        sol.forEach(i=>{
            ans.push([sub, ...i]);
        })
    }
    return ans;
};
function test(s){
    var l = s.length;
    var lim = l>>1;
    for(var i=0;i<lim;i++){
        if(s[i]!=s[l-1-i]){
            return false;
        }
    }
    return true;
}

子串

和为 K 的子数组

解法1：暴力前缀和

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var subarraySum = function (nums, k) {
    var pre = Array.from({ length: nums.length+1 }, () => 0);
    for (var i = 1; i <= nums.length; i++) {
        pre[i] = pre[i - 1] + nums[i-1];
    }
    var count = 0;
    for(var s = 0;s<nums.length;s++){
        var l_uppper = nums.length-s+1;
        for(var l = 1;l<l_uppper;l++){
            if(pre[s+l]-pre[s]==k){
                count++;
            }
        }
    }
    return count;
};

解法2：hash优化

解法1的瓶颈在于，对于某个指定的终点/起点，我们需要寻找减去起点后符合要求的起点/终点，从而导致又遍历了一次数组。由于k和起点在这一层循环定了下来，那么符合要求的pre[j]-k/pre[i]+k也是可确定的，只是不知道有多少符合条件，所以可以用hash表省去统计终点符合条件的起点/终点个数。

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var subarraySum = function (nums, k) {
    var map = new Map();
    map.set(0, 1); // 目标为0时可以是空数组，所以至少存在1个
    var pre = 0;
    var count = 0;
    var l = nums.length;
    // 向前统计起点
    for (var i = 0; i < l; i++) {
        pre += nums[i];
        var t = pre - k;
        if (map.has(t)) {
            count += map.get(t); 
        }
        map.set(pre, map.has(pre) ? (map.get(pre) + 1) : 1);
    }
    return count;
};

图论

常规搜索。

/**
 * @param {character[][]} grid
 * @return {number}
 */
var numIslands = function (grid) {
    var h = grid.length, w = grid[0].length;
    var count = 0;
    var sig = Array.from({ length: h }, () => Array.from({ length: w }, () => true))
    var dir = [[1, 0], [-1, 0], [0, 1], [0, -1]];
    var search = function (i, j) {
        if (i >= 0 && i < h && j >= 0 && j < w && sig[i][j]) {
            sig[i][j] = false;
            if (grid[i][j] == '1')
                for (var k = 0; k < 4; k++) {
                    search(i + dir[k][0], j + dir[k][1]);
                }
        }
    }
    for (var i = 0; i < h; i++) {
        for (var j = 0; j < w; j++) {
            if (sig[i][j]&&grid[i][j]=='1'){
                search(i,j);
                count++;
            }
        }
    }
    return count;
};

/**
 * @param {number[][]} grid
 * @return {number}
 */
var orangesRotting = function (grid) {
    var startMin = 0;
    var nextMin = 0;
    var queue = [];
    var h = grid.length, w = grid[0].length;
    var o_count = 0;
    for (var i = 0; i < h; i++) {
        for (var j = 0; j < w; j++) {
            if (grid[i][j] > 0) {
                o_count++;
                if (grid[i][j] == 2) {
                    queue.push([i, j]);
                }
            }
        }
    }
    var rot_count = queue.length;
    var last_rot_count = rot_count;
    var dir = [[0, 1], [0, -1], [1, 0], [-1, 0]];
    do {
        startMin = nextMin;
        last_rot_count = rot_count;
        var l = queue.length
        for (var i = 0; i < l; i++) {
            var pos = queue[i];
            for (var k = 0; k < 4; k++) {
                var _d = dir[k];
                var y = pos[0] + _d[0], x = pos[1] + _d[1];
                if (x >= 0 && x < w && y >= 0 && y < h && grid[y][x] == 1) {
                    grid[y][x] = 2;
                    rot_count++;
                    queue.push([y,x]);
                }
            }
        }
        nextMin++;
    } while (rot_count > last_rot_count);
    return o_count==rot_count?startMin:-1;
};